Transport in Freezing Soils

Understanding of freezing processes in northern regions is significant because of their impact on hydrologic processes and energy balance at the soil surface. Freezing of soil water near the surface blocks paths for surface water to infiltrate and increases runoff. It also presents a risk to damage plant roots, cause cracks in pavement, and damage the foundations of buildings due to frost heave effects. Another application of freezing is that it can be employed by man to assist in construction activities and environmental remediation, such as artificial ground freezing.

Thermal regelation in soils

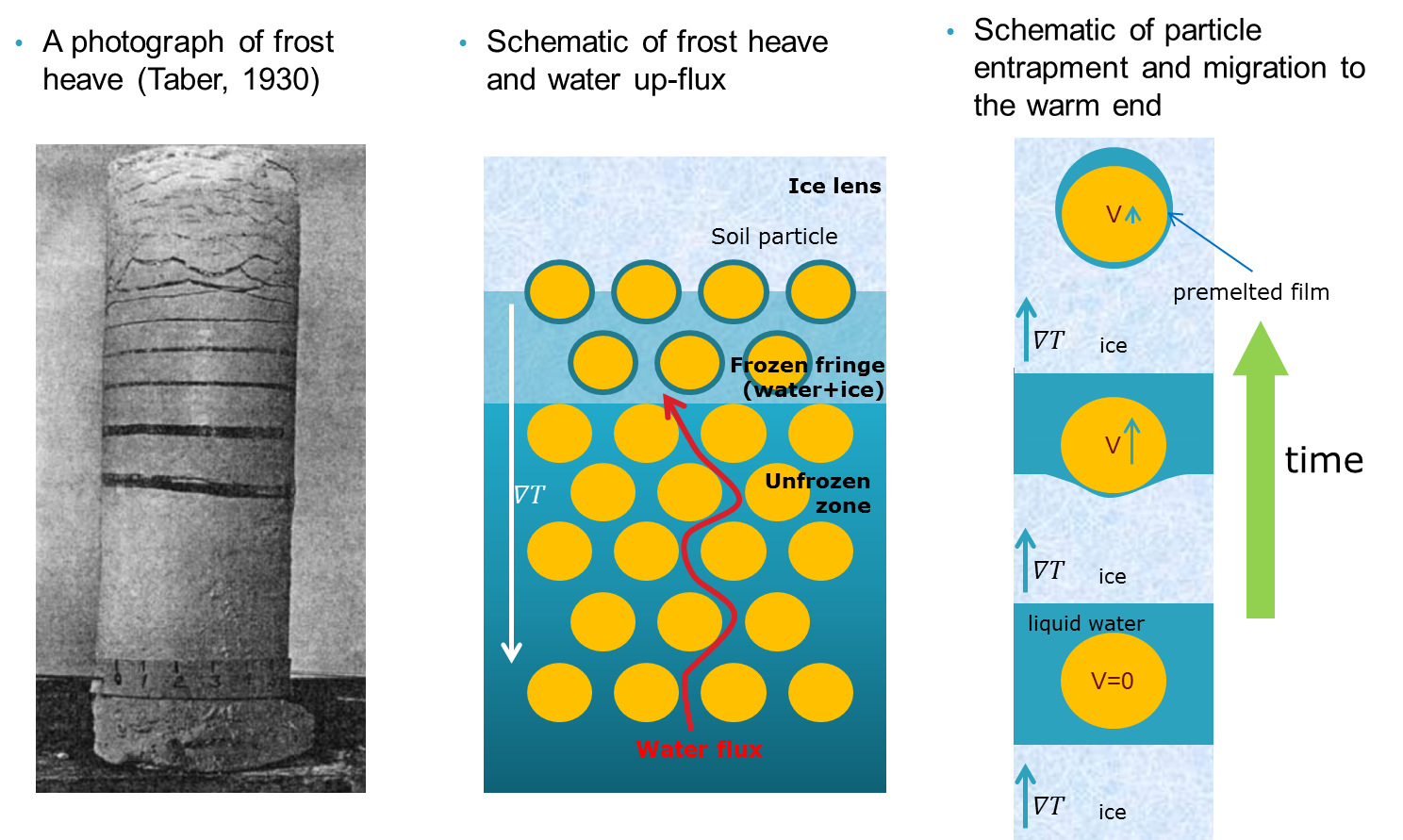
Frost heave is the process of uplifting of ground surface in water saturated soils due to the ice buildup in underlying layers of soil. Formation of ice in pore void in a freezing soil creates pore stresses that are capable of disjoining soil particles and exceeding an overburden pressure. Once majority of pore void is filled with ice, individual soil particles can travel upward from lower temperatures in the soil to higher temperatures at the surface during seasonal temperature variations in the atmosphere.

Individual particles enwrapped in ice can move due to a phenomenon called thermal regelation. A thin liquid premelting film surrounds a soil particle and separates it from ice. At the upper side of the particle, liquid film is subject to higher temperatures causing a partial melting of ice. The increased water pressure as a result of melting at that location causes a liquid water downward flux along the film and water freezes at the bottom. The ice formed under the particle forces the particle to move upward and travel toward the warmer soil layers.

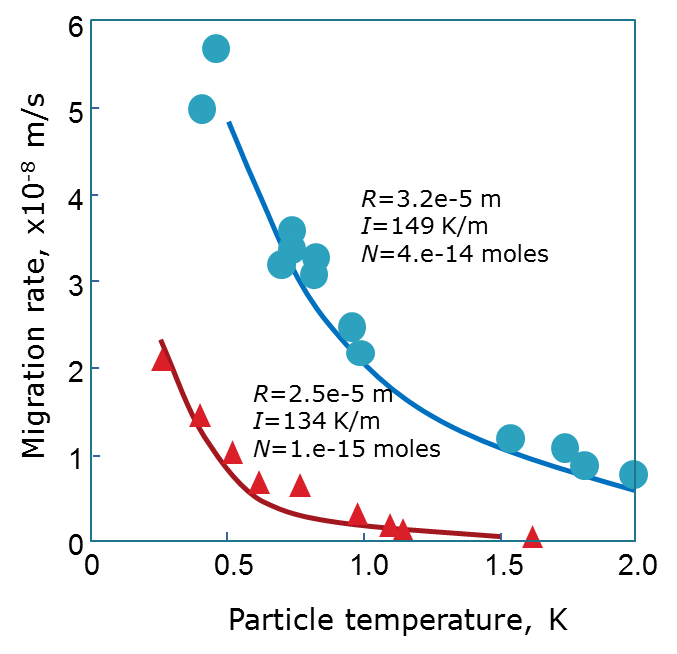
Two models were developed to model the thermal regelation phenomenon. Both models follow an assumption that the supercooled liquid film exists due to the intermolecular interactions creating nonretarded van-der-Waals forces that lower the temperature of film freezing. Additionally, the second model assumes that the liquid film contains impurities premelted from the surrounding ice. For the first model, an explicit closed form solution was foound that provided a relationship between the particle migration rates, physical properties of the system, and temperature gradient. The second model was more complex and required a numerical solution to be developed. Results provide a good agreement with the experiments by Romkens and Miller.

Freezing of soils due to applied subzero temperature at the soil surface results in the formation of a freezing front that progresses downward with time. The reduced liquid water content and liquid water pressure at and behind the freezing front induce water flow toward the zone behind the front and accumulation of ice therein. While freezing persists and progresses downward, more water is drawn from deeper horizons, increasing pore pressure behind the freezing front [Harlan, 1973]. When the pore pressure behind the freezing front exceeds the overburden pressure, the matrix structure at that point in the soil will break, thus allowing initiation of a pure ice layer or an ice lens. This lens then continues to accumulate ice as liquid water transfers toward it, thereby uplifting the soil above that depth and causing frost heave

Frozen walls in saturated soils

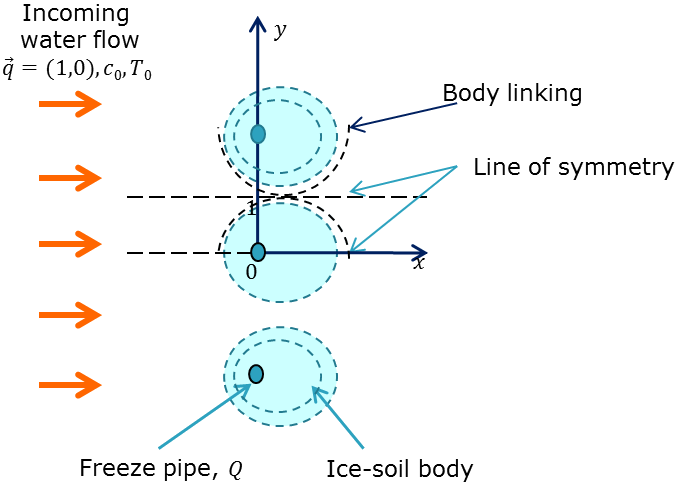
Modeling a coupled flow and heat and mass transport in freezing soils by means of classical approaches such as analytical solutions of a system of governing equations provides insights on freezing processes in soils. In a mathematical study on creation of frozen walls/barriers and their evolution we formulated a mathematical model by linking heat and mass transport equations with the thermodynamic equilibrium condition:

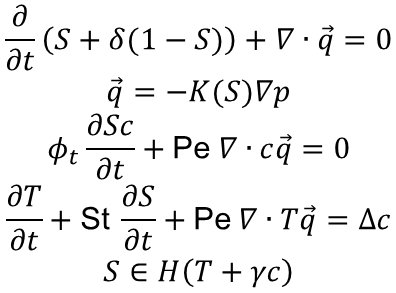
A numerical solution procedure by adopting a finite difference scheme with iterative Multigrid method was utilized for solving a system of the discretized equations. As soil water contained solute, the freezing temperature was lowered allowing a simultaneous presence of ice and unfrozen water at the same location within a domain. The formed 'frozen walls' were penetratible for unfrozen water and had water flows through them. Smaller the saturations of unfrozen water are, the more solid frozen walls are formed. The streamlines for water flux at a specific time are shown below:

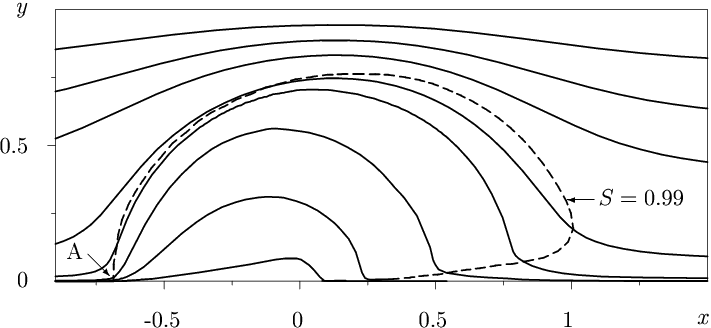
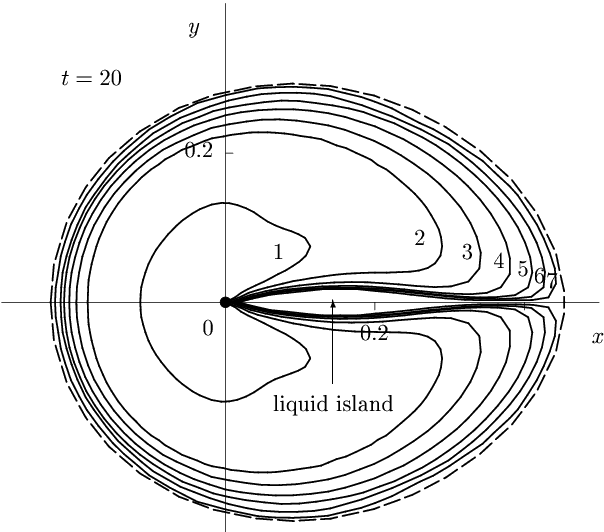
The modeling approach resulted in discovering interesting liquid intrusions within artificially created frozen walls. Lowering hydraulic permeability within the frozen wall along with a small liquid flow through it created a trapping zone for solute that do not allow solute to escape. Such trapping zones ('liquid islands') can cause stability issues for artificially generated frozen barriers in the soils.

Freezing in unsaturated soils

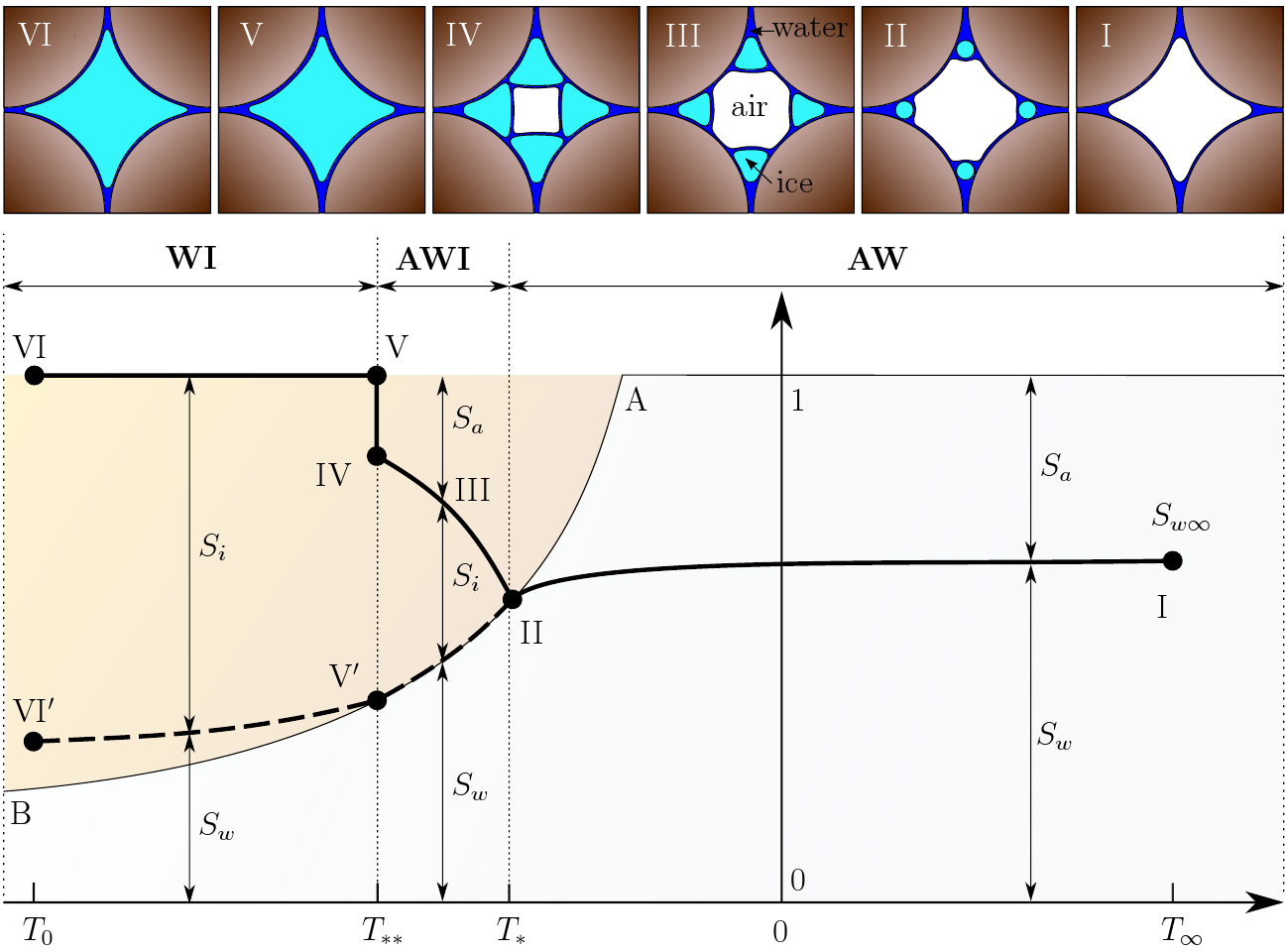
A mathematical model of heat and mass transport in partially-frozen variably-saturated soils was developed based on Miller's concept of equilibrium ice growth in pore-scale. The model is capable of describing a coupled heat and mass transport in three cobminations of air, water, and ice in soil pore voids. Three zones were disinguished:

• AW-zone contains air and water
• AWI-zone contains air, water and ice
• WI-zone contains ice and water

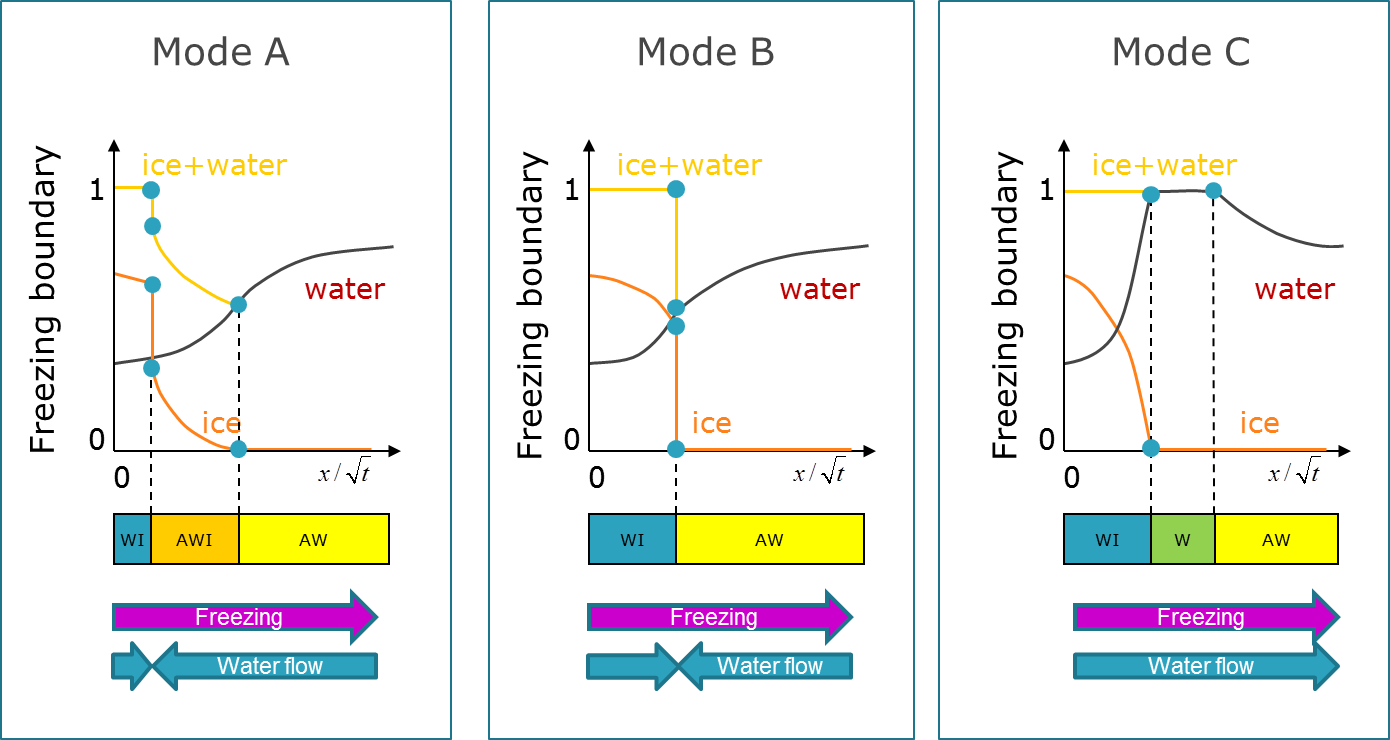
Freezing of unsaturated soils is associated with the formation of a moving freezing zone and liquid water flow toward the zone. An equilibrium thermodynamic formulation of coupled flow and heat transport in variably saturated partially frozen porous media is developed and a self-similar solution is derived for the case of a semi-infinite horizontal porous media column with a constant freezing temperature on one boundary. Solutions to the self-similar equations are derived using a Runge-Kutta solution procedure. The solution is found to yield three possible modes distinguished by three zones composed of different combinations of ice, liquid water, and air. One of the modes (A) contains three zones: a frozen WI zone; a transition AWI zone; and an unsaturated AW zone. The second mode (B) contains only the WI zone and the AW zone. It is found that the WI zone is a quintessential part of the solution. The AWI zone is found to exist when the advancement of the freezing zone is relatively fast, while it is absent when the zone advances slowly. The third mode (C) is found for a soil at or close to the saturated condition. An intermediate fully saturated unfrozen zone with water pressure above the air-entry pressure occurs between the frozen (WI) zone and unfrozen (AW) zone. All three modes are shown in the diagram below.

Pore pressure is calculated as a linear combination of ice pressure and liquid water pressure, and the calculated figures are used to provide a condition for model limitation in the case of incipient ice lens formation. The developed similarity solution provides insight into the mechanics of liquid water movement and pore filling with ice and the conditions for incipient heaving.

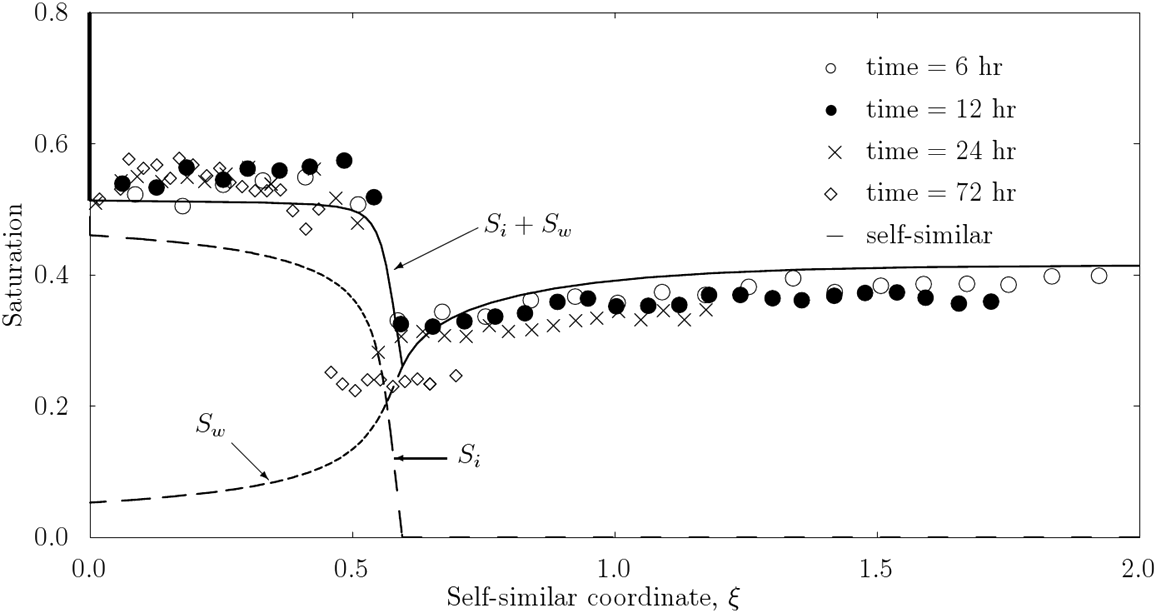
Predictions of ice saturation and liquid water saturation with the self-similar solution are compared to published experimental data. We used the experiments by Jame and Norum and converted the published data to self-similar coordinates used in the theoretical study. Simulations up to 48 hours provide reasonable basis for comparison, while the results for 72 hours demonstrate deviation in freezing front position and water saturation at the warm end from self-similar behavior. It occured due to the sample used being closed on both ends thus limiting the water flux toward the freezing front.

Relevant publications:

1. Sheshukov, A.Y. and J.L. Nieber (2011) Freezing of Nonheaving Unsaturated Soils: Model Formulation and Similarity Solution, Water Resources Research, 47. DOI:10.1029/2011WR010512
2. Sheshukov, A.Y. and A.G. Egorov (2002) Frozen barrier evolution in saturated porous media, Advances in Water Resources, 25(6), 681-689.
3. Sheshukov, A.Y., and A.G. Egorov (1998) Numerical modeling of coupled moisture, solute and heat transport in frozen soils, In: Proceedings of 7th International Conference on Permafrost, Yellowknife, Canada, 987-992.
4. Egorov, A.G., A. V. Kosterin, and A.Y. Sheshukov (1995) One-dimensional problems of frozen soil thawing due to solution seepage, Fluid Dynamics, 30, 767-776.
5. Egorov, A.G., A. V. Kosterin, and A.Y. Sheshukov (1993) Mathematical modelling of the motion of a solid inclusion in a nonisothermal block of ice, Colloid Journal of Russian Academy of Sciences, 55, 350-359.